
Hablemos un poco sobre teoría de grafos y sus implicaciones en la relación directa entre los nodos de redes inalámbricas, podría parecernos algo muy trivial y sin importancia, pero es un problema que ha costado mucho tiempo y esfuerzo, de hecho, en la actualidad no se tiene solución, sin embargo se están realizando estudios para entender mejor este problema y encontrarle solución.
Gracias a la forma en que están organizados los pelos de la mosca de la fruta, tiene el potencial de proporcionar la solución a los problemas que plantean las redes inalámbricas, ya que ésta es más simple y eficiente que cualquier red elaborada por el ser humano.
Mantener comunicados de forma eficiente dos computadoras es una tarea muy sencilla. Pero a medida que el número de computadoras de la red comienza a aumentar, la situación se complica. Las redes actuales suelen ser muy poco eficientes, sobre todo cuando el sistema de conexión elegido es el inalámbrico.
Teoría de grafos
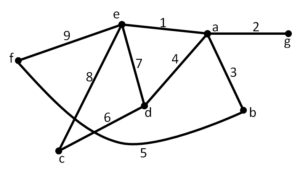
La Teoría de Grafos juega un papel importante en la fundamentación matemática de las Ciencias de la Computación. Los grafos constituyen un instrumento básico para modelar fenómenos
discretos y son fundamentales para el entendimiento de las estructuras de datos y el análisis de algoritmos. En matemáticas y ciencias de la computación, la teoría de grafos estudia las propiedades de los grafos, que son colecciones de objetos llamados vértices (o nodos) conectados por líneas llamadas aristas (o arcos) que pueden tener orientación (dirección asignada). Típicamente, un grafo está diseñado por una serie de puntos (los vértices) conectados por líneas (las aristas).
Grafo

Un grafo es una dupla G = (V, A), donde V es un conjunto de puntos, llamados vértices, y A es un conjunto de pares de vértices, llamadas aristas, ¿Fácil no?.
En teoría de grafos, sólo queda lo esencial del dibujo: las formas de las aristas no son relevantes, sólo importa a qué vértices están unidas. La posición de los vértices tampoco importa, y se puede variar para obtener un grafo más claro.
Generalmente, se considera que colocar los vértices en forma de polígono regular da grafos muy legibles. Prácticamente cualquier red puede ser modelada con un grafo: una red de carreteras que conecta ciudades, una red eléctrica o un alcantarillado y por supuesto una red inalámbrica.
Conjunto independiente o estable
Ahora que ya sabemos lo que es un grafo entremos más en materia. Un conjunto independiente o estable es un conjunto de vértices en un grafo tal que ninguno de sus vértices es adyacente (Que está muy próximo o unido a) a otro. Es decir, es un conjunto V de vértices tal que para ningún par de ellos existe alguna arista que los conecten. En otras palabras, cada arista en el grafo contiene a lo más un vértice en V. El tamaño de un conjunto independiente es el número de vértices que contiene. Creo que la cosa se complica un poco.
Conjunto independiente maximal
Enfoquémonos en lo que las moscas nos pueden ayudar. Un conjunto independiente maximal es un conjunto independiente tal que, añadiendo cualquier otro vértice al conjunto, éste deja de ser independiente, ¿Claro no?
Bueno dejémonos de tanto rollo y hagámoslo más legible.
Al igual que en una red de ordenadores basada en la arquitectura cliente-servidor, las células del sistema nervioso de la mosca de la fruta se organizan de tal manera que un pequeño porcentaje de ellas funcionen como “centros” (vértices) que proporcionan las conexiones (aristas) necesarias con las demás células nerviosas. En base a esta relación, se creó un algoritmo informático que imita esta forma de trabajo, y descubrieron que esta manera de constituirse puede utilizarse para optimizar aquellas redes de ordenadores en las que el número y posición de los nodos que la componen no están rígidamente establecidos.
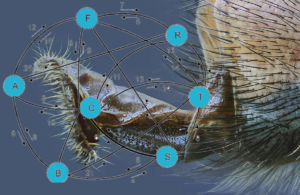
Los principales servicios que se beneficiarían serían las redes WIFI, los sistemas de recolección de datos basados en sensores inalámbricos o grupos de robots autónomos. Noga Alon, experto en matemática e informática de la Tel Aviv University y del Institute for Advanced Study de Princeton, Estados Unidos, coautor del artículo, explica que “se trata de una solución tan simple e intuitiva que cuesta creer que no hayamos descubierto su valor 25 años antes”.
“La mosca de la fruta posee en la superficie de su cuerpo un conjunto de pelos que actúan a modo de sensores mecánicos detectores de movimiento. Algunos de estos pelos más pequeños, denominados microsetas, se desarrollan a partir de un grupo de neuronas que son precursores de órganos sensoriales (POS).”
Los expertos se basaron en una estrategia muy conocida por muchos de nosotros, el famoso juego de buscaminas, si alguna vez llegaste a jugarlo, entenderás mejor este problema.

Inicialmente podemos seleccionar cualquier casilla del juego (en gris). Cuando elegimos como POS una de las células aleatoriamente (en azul) las de su alrededor quedan marcadas (en rojo), porque lo que ya no pueden elegirse en el siguiente paso, exactamente igual al buscaminas.
Así es como los investigadores desarrollaron el algoritmo para el cálculo del Conjunto independiente maximal. Esto lo hace aplicable a problemas en los que la topología del grafo es variable, como los citados.
Fuente:[Naukas][emol][cmu][ScienceMag] Matemáticas Discretas, Teoría de grafos, Tec de Monterey, Campus Cuernavaca.

